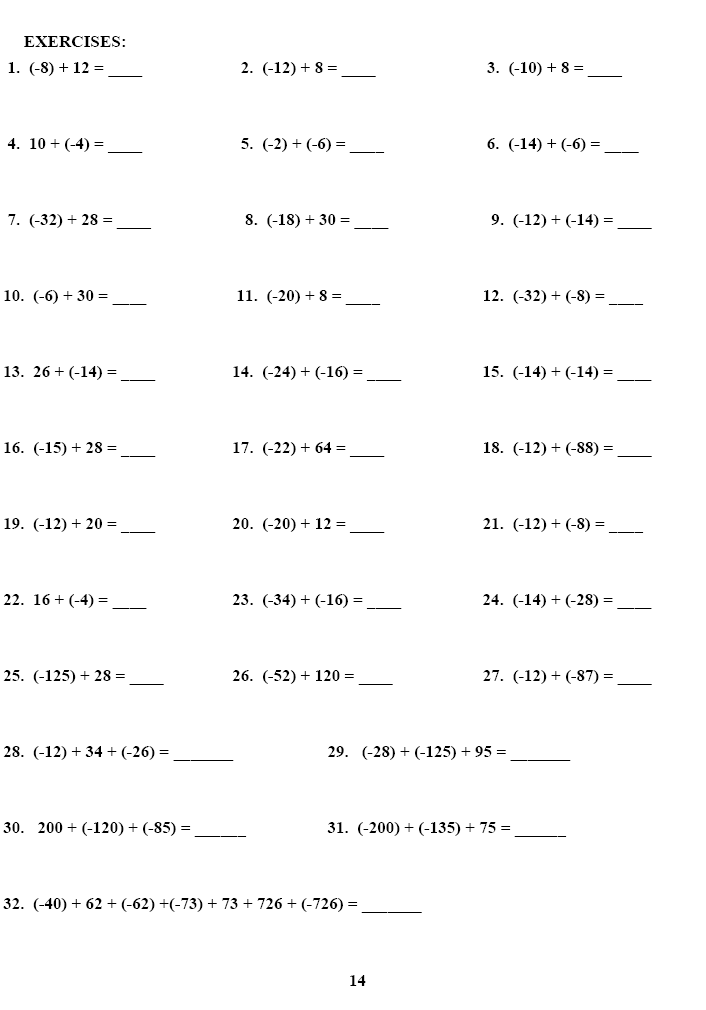Are you navigating the world of Analytic Geometry Grade 10 Worksheets and feeling a bit lost? Fear not! We’re here to guide you through this fascinating mathematical landscape with clarity and confidence. Analytic Geometry, while it may seem intimidating at first, is a rewarding subject that lays the foundation for understanding advanced mathematical concepts. Let’s embark on this journey together and unlock the secrets of Analytic Geometry Grade 10 Worksheets.
Understanding Analytic Geometry Grade 10 Worksheets
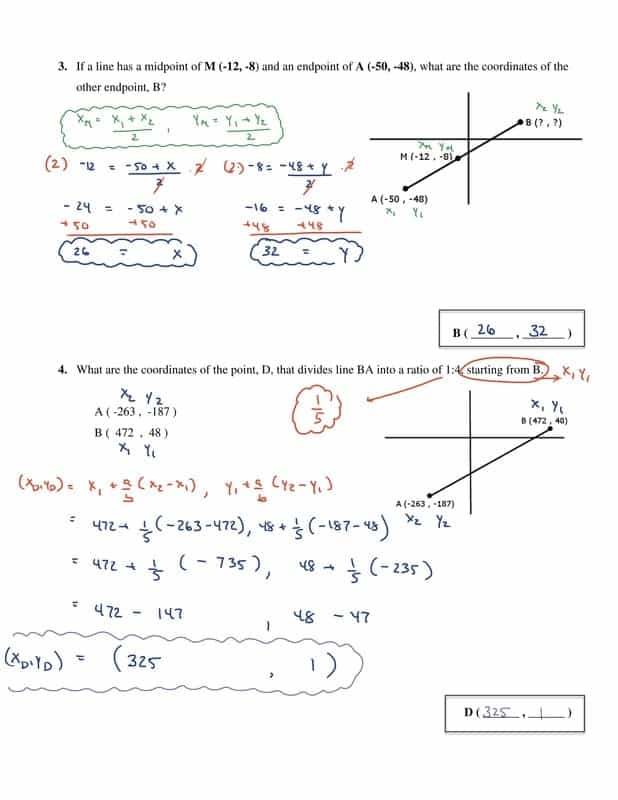
Analytic Geometry Grade 10 Worksheets delve into the study of geometric shapes using a coordinate system. This branch of mathematics combines algebraic techniques with geometric concepts, providing a powerful toolset to analyze shapes and their properties. In Grade 10, students typically encounter fundamental topics such as points, lines, angles, and equations of lines and circles.
Essential Concepts to Master
- Coordinate Geometry
The cornerstone of Analytic Geometry, coordinate geometry involves representing geometric figures using coordinates. Understanding how to plot points on a Cartesian plane and derive equations of lines and circles is crucial. - Equations of Lines
Mastering the slope-intercept form (y = mx + b) and point-slope form (y – y₁ = m(x – x₁)) of linear equations is essential. Students learn to identify slope, intercepts, and relationships between different lines. - Equations of Circles
Exploring the standard form of a circle’s equation (x – h)² + (y – k)² = r², where (h, k) represents the center and r denotes the radius, is key. Understanding the properties of circles and their graphical representations is fundamental. - Conic Sections
Introducing students to conic sections such as parabolas, ellipses, and hyperbolas opens doors to deeper mathematical exploration. Learning their standard equations and geometric properties broadens the scope of Analytic Geometry.
Practical Tips for Success
- Practice Regularly
Consistent practice is vital for mastering Analytic Geometry. Work through a variety of worksheets, problems, and exercises to reinforce concepts and improve problem-solving skills. - Understand the Theory
Don’t just memorize formulas; strive to understand the underlying theory. Visualize geometric shapes, explore their properties, and grasp the reasoning behind mathematical principles. - Seek Clarification
Don’t hesitate to seek help if you encounter difficulties. Reach out to your teacher, classmates, or online resources for clarification on challenging topics. - Utilize Resources
Take advantage of online resources, textbooks, and supplementary materials to enhance your learning experience. Websites, videos, and interactive tutorials can provide valuable insights and explanations.
Resources for Further Exploration
- Online Worksheets
Explore a plethora of Analytic Geometry Grade 10 Worksheets available online. Websites like Khan Academy, Math Worksheets 4 Kids, and IXL offer a wide range of practice exercises catering to different skill levels. - Textbooks
Refer to standard Grade 10 mathematics textbooks for comprehensive coverage of Analytic Geometry concepts. Textbooks often provide detailed explanations, examples, and practice problems to reinforce learning. - Educational Apps
Engage with educational apps that gamify learning and make studying Analytic Geometry enjoyable. Apps like GeoGebra, Desmos, and Photomath offer interactive tools and visualizations to aid comprehension.
Exploring Advanced Topics
As you progress in your study of Analytic Geometry Grade 10 Worksheets, you’ll encounter more advanced topics that build upon the foundational concepts. Let’s delve into some of these areas:
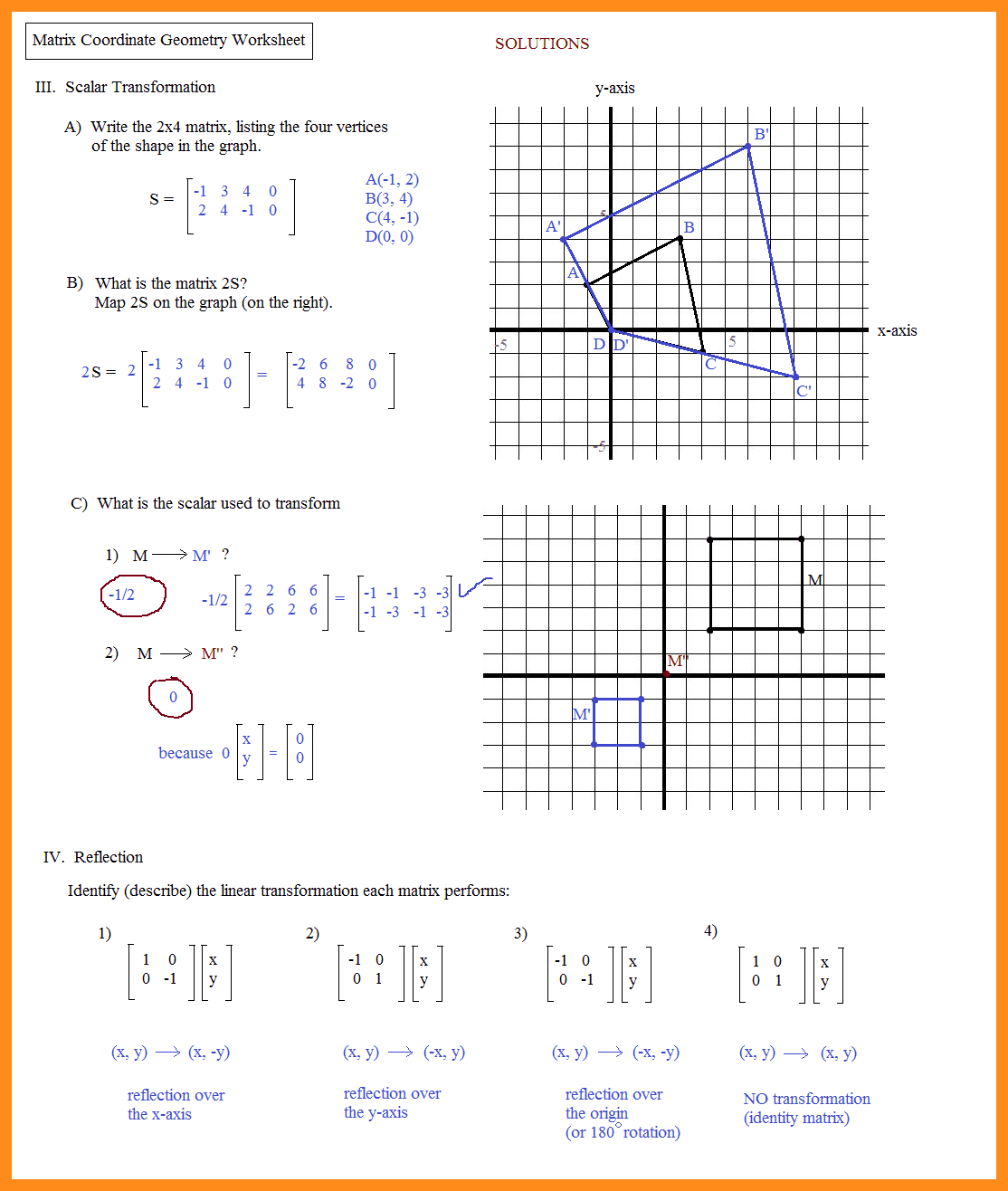
- Transformational Geometry
Explore transformations such as translations, reflections, rotations, and dilations. Understanding how these transformations affect geometric figures helps deepen your understanding of symmetry, congruence, and similarity. - Three-Dimensional Geometry
Extend your knowledge beyond the two-dimensional plane into three-dimensional space. Learn about points, lines, planes, and solids, and how to analyze their properties using coordinates and equations. - Vectors
Introduce yourself to the concept of vectors and their applications in Analytic Geometry. Explore vector operations, scalar multiplication, dot and cross products, and their geometric interpretations. - Analytic Proofs
Develop your ability to construct and communicate mathematical arguments using analytical techniques. Practice writing proofs to justify geometric assertions and deepen your understanding of mathematical reasoning.
Interactive Learning Opportunities
In addition to traditional methods of learning, consider incorporating interactive and engaging activities into your study routine. Here are some suggestions:
- Interactive Graphing Tools
Experiment with online graphing calculators and software that allow you to visualize geometric concepts dynamically. Manipulate graphs, plot points, and explore transformations in real-time. - Collaborative Problem-Solving
Form study groups or join online communities where you can collaborate with peers to solve challenging problems. Discuss different approaches, share insights, and learn from each other’s perspectives. - Real-World Applications
Explore real-world applications of Analytic Geometry to deepen your appreciation for its relevance. Investigate how geometric concepts are utilized in fields such as engineering, architecture, physics, and computer graphics. - Creative Projects
Undertake creative projects that integrate Analytic Geometry with other disciplines or personal interests. Design geometric artwork, create models of architectural structures, or develop geometric puzzles and games.
Embracing Challenges and Celebrating Progress
As you navigate through Analytic Geometry Grade 10 Worksheets, it’s important to embrace challenges as opportunities for growth. Don’t be discouraged by setbacks or moments of confusion; instead, view them as stepping stones on your journey towards mastery.
Celebrate your progress and achievements along the way, no matter how small they may seem. Each problem solved, concept understood, and skill honed is a testament to your dedication and perseverance. Remember that learning is a continuous process, and every experience contributes to your development as a mathematician and critical thinker.

By approaching Analytic Geometry Grade 10 Worksheets with curiosity, determination, and a willingness to learn, you’ll not only excel academically but also cultivate a deeper appreciation for the beauty and elegance of mathematics. So, roll up your sleeves, sharpen your pencils, and embark on this exciting mathematical adventure with confidence and enthusiasm. The world of Analytic Geometry awaits!